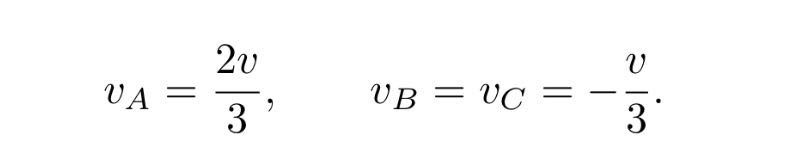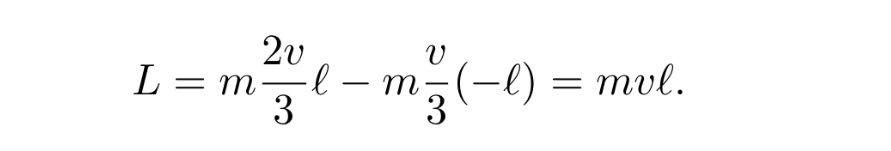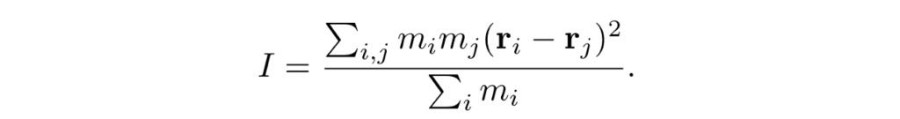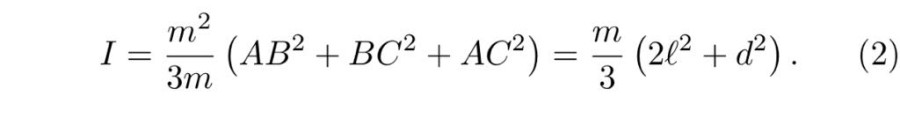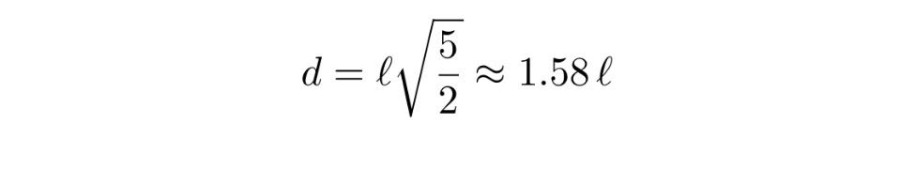Успехи и постижения

Българският национален отбор по физика се завърна с 5 медала от Европейската олимпиада по физика (EuPhO), провела се от 28 май до 1 юни в малък град близо до Москва. Всеки от петимата гимназисти, взели участие в олимпиадата, получи отличие:

Георги Александров – СМГ, 11 клас – златен медал;

Таквор Баронян – Darbi College гр. София, 12 клас – сребърен медал;

Стефан Иванов – ППМГ „Никола Обрешков“, гр. Бургас – сребърен медал;

Иво Петров – ПГПАЕ, гр. Бургас, 10 клас – бронзов медал;

Руско Русков – ПГПАЕ, гр. Бургас, 12 клас – бронзов медал.

Техен ръководител на олимпиадата бе Нено Тодоров от Физическия факултет на Софийския университет „Св. Климент Охридски“, специализиращ в електрични, магнитни и оптични свойства на кондензираната материя (вкл. оптични свойства и спектроскопия на кондензираните среди).

Европейската олимпиада по физика е състезание за гимназисти, което се организира отделно от Международната олимпиада в тази област (провела за се пръв път през 1967). Тазгодишното издание на това състезание е едва второто – през 2017 в Естония е било откриването на тази европейска олимпиада.

Участниците в олимпиадата се доближават възможно много до действителни условия на научни изследвания. Описанието на всяка задача, над която участниците трябва да размишляват и да покажат своите знания, е възможно най-кратко, за да може те да покажат творчество и въображения при решаването на задачите. 

Тук може да видите пример за задача*, давана в раздел "теория" на тазгодишното издание на състезанието:

Три еднакви топчета, наименовани A, B и C са свързани посредством две еднакви пръчици с обща дължина 2l. Масата на всяко топче е m, а тази на пръчиците е пренебрежимо малка и може да се счита за равна на нула. Едната пръчица свързва А и В, а другата В и С. Връзката между двете пръчици при топче В е такава, че ъгълът между двете пръчици може да се променя свободно. Системата  в безтегловност, така че всички нейни елементи лежат в една равнина. Топче А е задвижено със скорост, перпендикулярна на пръчиците.
Намерете минималното разстояние d между А и С по време на последвалото движение на системата. Всяко триене да се пренебрегне.

*Решението на задачата можете да намерите в края на статията.

Както медалистите, така и техният ръководител господин Тодоров споделиха, че са изключително доволни от представянето си на състезанието, пише MediaBricks.bg. Представянето на България е било по-успешно от същото на миналото издание на състезанието, въпреки голямата конкуренция - българските ученици са се борили срещу 115 техни връстници от 23 държави, сред които Азербайджан, Белгия, Босна и Херцеговина, Бразилия, Хърватия, Чехия, Естония, Германия, Унгария, Италия, Казахстан, Латвия, Македония, Румъния, Русия, Словакия, Словения, Швеция, Швейцария, Таджикистан и Турция.

Преподавателите, подготвяли медалистите ни, са с голям принос за успехите. Между тях са както Георги Стойчев (ППМГ, гр. Бургас), Илиян Петров и Стоян Бахчеванов (СМГ) и Венета Манева (ПГПАЕ, гр. Бургас), така и Теодосий Теодосиев, от чиято школа в гр. Казанлък са излезли златни медалисти по природни науки, прославили България по целия свят.

Олимпиадата се проведе на две нива – теоретическа и практическа част. Програмата на събитията в рамките на състезанието беше организирана така, че участниците да могат не само да покажат знанията и уменията си на теория и на практика, но да установят контакт със своите връстници от други части на света и да се запознаят с чужди култури и обичаи. Те имаха възможност да посетят музея на космонавтиката в Москва, посветен на напредъка на руските учени в изучаването на Космоса, както и театрално представление.

Това състезание е от особена важност за младите физици по целия свят, не само защото ги предизвиква да използват както знанията си, така и способността си да мислят творчески, но и защото им дава нещо повече от медал или постижение – култура. Културата е неразривна част от всеки народ, и досега с културата и с науката едновременно учи на благородство, патриотизъм и други добродетели. При досега с наука и култура едновременно учениците осъзнават, че те могат да са следващите, направили велики открития в научната сфера и че за това трябва да познават колкото може повече аспекти на живота. Пожелаваме им да дерзаят, да не се отказват от мечтите си и да прославят страната ни все повече и повече!

Решение на задачата, дадена за пример по-горе:

Означаваме скоростта, с която топче А се движи по ос Y с буквата v. Импулсът на системата се запазва, следователно центъра на масите на системата (CM) се движи по ос Y с постоянна скорост - v.

Системата е инертна, следователно тук важат законите за запазване на енергията, на импулса и на ъгловия момент. Началните скорости на трите топчета са:

Съответно, общата кинетична енергия на топчетата, означена с Е, е равна на:

а общия ъглов момент, е равен на:

Във всеки един момент трите топчета формират равнобедрен триъгълник (пръчиците са равни по дължина - l) и един от ъглите е 2β, а другите два са равни помежду си. Разстоянието между А и С е минимално, само когато или β е равен на нула, или β` е равно на нула (β` = 180° - β). Ако β е равно на нула обаче, то законите за запазване на енергията, на импулса и на ъгловия момент не са съвместими с постоянното положение и постоянната скорост на елементите в системата. Следователно, β` е равно на нула и в този определен случай системата може да се разглежда като неподвижно тяло, чийто инертен момент може да се определи като използваме стойността на центъра на масите:

От друга страна, инертният момент I може да се изчисли независимо от геометричните зависимости. Въпреки това, стойността на I може да се намери посредством стойностите на разстоянията от топчетата до центъра на масите – центъра на медианите в равнобедрения триъгълник. По-удобно е да използваме тази формула за инертния момент на сбор от маси на точки (в случая - топчета), в която се използва и центъра на масите.

В този определен случай от горната формула се получава това:

Като имаме предвид (1) и (2), можем да изчислим и минималното разстояние d:

Надяваме се, че сме предизвикали интереса ви! Ако искате да научите повече, или да пробвате други задачи от олимпиадата, можете да го направите ТУК!