–Ь–∞—В–µ–Љ–∞—В–Є—Ж–Є—В–µ –Р–љ–і—А—О –Ы–Њ–± –Є –Ф–ґ–Њ—И—Г–∞ –У—А–Є–є–љ —Б—К—Г–Љ—П–≤–∞—В –і–∞ —Б–µ —Б–њ—А–∞–≤—П—В —Б –љ–µ—А–µ—И–µ–љ–∞—В–∞ –Ј–∞–і–∞—З–∞ –њ–Њ –≤—А–µ–Љ–µ –љ–∞ –њ–∞–љ–і–µ–Љ–Є—П—В–∞. –Ґ–µ –Ј–∞–њ–Њ—З–≤–∞—В —Б–≤–Њ—П—В–∞ —А–∞–±–Њ—В–∞ –≤ —Б—А–µ–і–∞—В–∞ –љ–∞ –Љ–∞—А—В, –∞ –і–≤–∞ –Љ–µ—Б–µ—Ж–∞ –њ–Њ-–Ї—К—Б–љ–Њ –њ—Г–±–ї–Є–Ї—Г–≤–∞—В —А–µ—И–µ–љ–Є–µ—В–Њ —Б–Є.
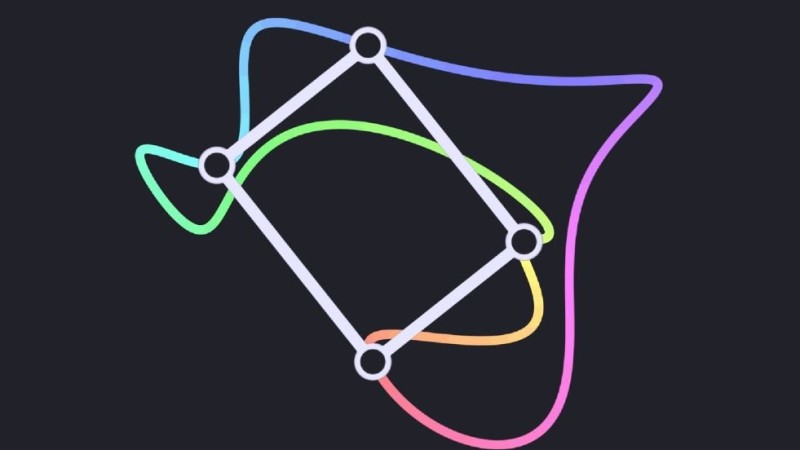
–Ф–ґ–Њ—И—Г–∞ –У—А–Є–є–љ –Є –Р–љ–і—А—О –Ы–Њ–± –њ—Г–±–ї–Є–Ї—Г–≤–∞—В —А–µ—И–µ–љ–Є–µ—В–Њ –љ–∞ –Є–Ј–≤–µ—Б—В–љ–∞—В–∞ –Ј–∞–і–∞—З–∞ –Ј–∞ –≤–њ–Є—Б–∞–љ–Є –њ—А–∞–≤–Њ—К–≥—К–ї–љ–Є—Ж–Є –љ–∞ 19 –Љ–∞–є. –Ч–∞–і–∞—З–∞—В–∞ –Ј–∞–і–∞–≤–∞ –≤—К–њ—А–Њ—Б–∞ –і–∞–ї–Є –µ –≤—К–Ј–Љ–Њ–ґ–љ–Њ –≤ –Ј–∞—В–≤–Њ—А–µ–љ –Ї–Њ–љ—В—Г—А –і–∞ —Б–µ –љ–∞–Љ–µ—А—П—В –≤–Є–љ–∞–≥–Є —З–µ—В–Є—А–Є —В–Њ—З–Ї–Є, –Ї–Њ–Є—В–Њ –і–∞ –Њ–њ—А–µ–і–µ–ї—П—В –≤—К—А—Е–Њ–≤–µ—В–µ –љ–∞ –њ—А–∞–≤–Њ—К–≥—К–ї–љ–Є–Ї —Б –њ—А–µ–і–≤–∞—А–Є—В–µ–ї–љ–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Њ —Б—К–Њ—В–љ–Њ—И–µ–љ–Є–µ –љ–∞ —Б—В—А–∞–љ–Є—В–µ.
–Э–∞ –њ—А—К–≤ –њ–Њ–≥–ї–µ–і –њ—А–Њ–±–ї–µ–Љ—К—В –Ј–∞ –≤–њ–Є—Б–∞–љ–Є—В–µ –њ—А–∞–≤–Њ—К–≥—К–ї–љ–Є—Ж–Є –Є–Ј–≥–ї–µ–ґ–і–∞ –µ–ї–µ–Љ–µ–љ—В–∞—А–µ–љ, –љ–Њ —В–Њ–є –µ —Г—Б–њ—П–ї –і–∞ –Ј–∞—В—А—Г–і–љ–Є –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –±–µ–ї–µ–ґ–Є—В–Є —Г–Љ–Њ–≤–µ –њ—А–µ–Ј –њ–Њ—Б–ї–µ–і–љ–Є—В–µ —Б—В–Њ –≥–Њ–і–Є–љ–Є.
–Э–∞—З–∞–ї–Њ—В–Њ –љ–∞ –Ј–∞–і–∞—З–∞—В–∞ –µ –њ–Њ—Б—В–∞–≤–µ–љ–Њ –Њ—В –љ–µ–Љ—Б–Ї–Є—П –Љ–∞—В–µ–Љ–∞—В–Є–Ї –Ю—В–Њ –Ґ–Њ–њ–ї–Є—Ж –њ—А–µ–Ј 1911 –≥. –Ґ–Њ–є –њ—А–µ–і–њ–Њ–ї–∞–≥–∞, —З–µ –≤—Б—П–Ї–∞ –Ј–∞—В–≤–Њ—А–µ–љ–∞ –Ї—А–Є–≤–∞ —Б—К–і—К—А–ґ–∞ —З–µ—В–Є—А–Є —В–Њ—З–Ї–Є, –Ї–Њ–Є—В–Њ, —Б–≤—К—А–Ј–∞–љ–Є, –Њ–±—А–∞–Ј—Г–≤–∞—В –Ї–≤–∞–і—А–∞—В. –Ф–Њ–Ї–∞—В–Њ –њ—А–µ–і–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ—В–Њ –Ј–∞ –≤–њ–Є—Б–∞–љ–Є—В–µ –Ї–≤–∞–і—А–∞—В–Є –±—К—А–Ј–Њ –µ –і–Њ–Ї–∞–Ј–∞–љ–Њ –Ј–∞ –љ–µ–њ—А–µ–Ї—К—Б–љ–∞—В–∞ (–±–µ–Ј —А–∞–Ј–Ї—К—Б–≤–∞–љ–Є—П) –Є –≥–ї–∞–і–Ї–∞ (–±–µ–Ј —К–≥–ї–Є) –Ј–∞—В–≤–Њ—А–µ–љ–∞ –Ї—А–Є–≤–∞ –њ—А–µ–Ј 1929 –≥., –Ј–∞–і–∞—З–∞—В–∞ –≤—Б–µ –Њ—Й–µ –љ–µ –µ —А–µ—И–µ–љ–∞ –Ј–∞ –љ–µ–њ—А–µ–Ї—К—Б–љ–∞—В–Є –љ–µ–≥–ї–∞–і–Ї–Є –Ї—А–Є–≤–Є.
–Ч–љ–∞—З–Є–Љ –љ–∞–њ—А–µ–і—К–Ї –њ–Њ –њ—А–Њ–±–ї–µ–Љ–∞ —Б –њ—А–∞–≤–Њ—К–≥—К–ї–љ–Њ—В–Њ –≤–њ–Є—Б–≤–∞–љ–µ –µ –њ–Њ—Б—В–Є–≥–љ–∞—В –≤ –і–Њ–Ї–∞–Ј–∞—В–µ–ї—Б—В–≤–Њ –љ–∞ –•—К—А–±—К—А—В –Т–Њ–љ –Њ—В –Ї—А–∞—П –љ–∞ 70-—В–µ –≥–Њ–і–Є–љ–Є . –Ґ–Њ –Є–љ–Є—Ж–Є–Є—А–∞ –љ–Њ–≤ –љ–∞—З–Є–љ –љ–∞ –Љ–Є—Б–ї–µ–љ–µ –≤ –≥–µ–Њ–Љ–µ—В—А–Є—П—В–∞ –љ–∞ –њ—А–∞–≤–Њ—К–≥—К–ї–љ–Є–Ї–∞ –Є —Г—Б—В–∞–љ–Њ–≤—П–≤–∞ –Љ–µ—В–Њ–і–Є, –Ї–Њ–Є—В–Њ –Љ–љ–Њ–≥–Њ –Љ–∞—В–µ–Љ–∞—В–Є—Ж–Є, –≤–Ї–ї—О—З–Є—В–µ–ї–љ–Њ –У—А–Є–є–љ –Є –Ы–Њ–±, –≤–њ–Њ—Б–ї–µ–і—Б—В–≤–Є–µ –Є–Ј–±–Є—А–∞—В.
–Ф–ґ–Њ—И—Г–∞ –У—А–Є–є–љ –µ –њ—А–Њ—Д–µ—Б–Њ—А –≤ Boston College –Є —А–∞–±–Њ—В–Є –≤ –Њ–±–ї–∞—Б—В—В–∞ –љ–∞ –љ–Є—Б–Ї–Њ–Љ–µ—А–љ–∞—В–∞ —В–Њ–њ–Њ–ї–Њ–≥–Є—П, –Ї–Њ—П—В–Њ –µ —Б–≤—К—А–Ј–∞–љ–∞ —Б—К—Б —Б–≤–Њ–є—Б—В–≤–∞—В–∞ –љ–∞ —Д–Њ—А–Љ–Є—В–µ. –Р–љ–і—А—О –Ы–Њ–± –њ—К–Ї –њ—А–µ–њ–Њ–і–∞–≤–∞ –≤ Durham University, –Ї–∞—В–Њ —Б–њ–Њ–і–µ–ї—П –Є–љ—В–µ—А–µ—Б–∞ –≤ –Њ–±–ї–∞—Б—В—В–∞ –љ–∞ –љ–Є—Б–Ї–Њ–Љ–µ—А–љ–∞—В–∞ —В–Њ–њ–Њ–ї–Њ–≥–Є—П.
–Ы—О–±–Њ–њ–Є—В–љ–Є—В–µ —З–Є—В–∞—В–µ–ї–Є –Љ–Њ–≥–∞—В –і–∞ —Б–µ –Ј–∞–њ–Њ–Ј–љ–∞—П—В –њ–Њ-–њ–Њ–і—А–Њ–±–љ–Њ –Є –љ–∞–≥–ї–µ–і–љ–Њ —Б—К—Б –Ј–∞–і–∞—З–∞—В–∞ –љ–∞ —Б–∞–є—В–∞ –љ–∞ –Э–∞—Г–Ї–∞ OFFNews –Є–ї–Є –і–∞ —А–∞–Ј–≥–ї–µ–і–∞—В —Б–∞–Љ–Є —А–µ—И–µ–љ–Є–µ—В–Њ –љ–∞ –і–≤–∞–Љ–∞—В–∞ –Љ–∞—В–µ–Љ–∞—В–Є—Ж–Є.
–Ш–Ј—В–Њ—З–љ–Є–Ї: –Э–∞—Г–Ї–∞ OFFNews